reality

Shamir did the job for you, just connect to the challenge and get the flag.

Time

8 hours

Actually, it only tooks me 1.5 hour to solve it after getting into the right direction.
I wasted a lot of time guessing the code and poking its PRNG 😡.

Behavior

Here's a base32-encoded and encrypted flag: DUHUKDEVNOPMLPYNJGHSAFJECOSJPUNENVP5J2NCJGADRLT7CRZQ====
To decrypt it you need 5 coefficients. I'll only give you 3
coefficients 1: 1.0922~[491 more digits]~5705, 717~[33 more digits]~542.4453~[453 more digits]~0219
coefficients 2: 1.1527~[491 more digits]~1035, 808~[33 more digits]~638.0541~[453 more digits]~6787
coefficients 3: 1.9277~[491 more digits]~3298, 345~[33 more digits]~353.7075~[453 more digits]~1995

We don't have any source code in this challenge. According to the description, it may uses shamir secret sharing to split the key into 5 pieces. However, we only have 3 of them.

Solution

TL;DR

Guess what the service does
Multiply $10^{450}$ to each number and truncate the fraction to integer
Build the lattice
Run LLL to find the shortest integer solution
Decrypt the flag with AES-CBC

Shamir secret sharing is used to split a secret into multiple pieces. It has two parameters, $n$ and $k$ . The secret will be split into $n$ pieces, and you'll need $k$ pieces to reconstruct the secret. Furthermore, you won't gain any knowledge of the secret with less than $k$ pieces (when implemented correctly).

Technically, it defines a polynomial of degree $k - 1$ :

$f(x) = \sum_{i=0}^{k-1} s_i x^i$

where $s_0$ is the secret and all other coefficients are randomly generated. Those split secret pieces are the points on this curve. We'll need at least $k$ points to reconstruct the curve, and it can be done using lagrange polynomial.

Typically, the shamir secret sharing works in a finite field instead of the reals. The precision in this task is pretty high, which gives us excessive information about the secret.

To solve this task, you have to guess that the coefficients are positive integers and they're quite small (~40 digits compares to 500 digits fraction).

I'll talk about the analysis before I came up with this guess. You can jump to the last section about LLL if you aren't interesting on the reason.

Random numbers

Without any knowledge about the service, I start from dumping 3000 pairs from the server and analyze how they are generated.

I dump with 16 threads in parallel, and I found that some output are the same. The collision probability is about 0.03, and all collisions only happened in succesive runs. It means the server may use a time-seeded PRNG (possible milliseconds).

Next I trying to figure out how they generate x, Here's the distribution of x I got from the server.

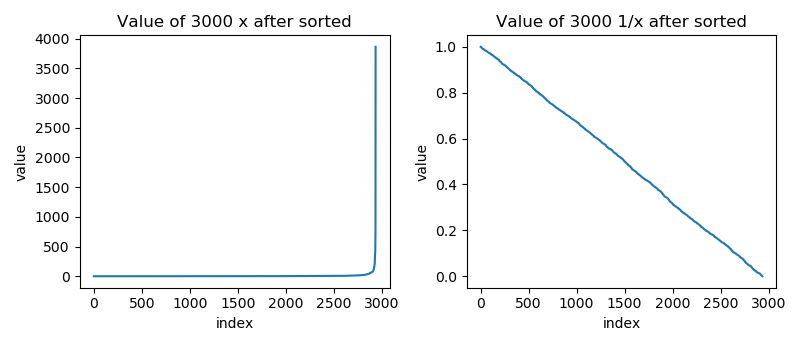
x_dist

Most of the x are closed to 1, and all of them are bigger than 1. The distribution of 1/x seems to be uniform distribution.

Moreover, the number of 1/x looks like:

0.5372495835723414270290732019930146634578704833984375
0.1468025157144856596147519667283631861209869384765625
0.39606395612572253828176371825975365936756134033203125

They are actually generated by rangrange(2^53) / 2^53.

Now we know how x are generated, how about the coefficients?

Random Coefficients

According to the polynomial of Shamir secret sharing, the expected value of these cofficients will be $f(x) / \sum_i x^i$ , which is about 225568696201524096821742572483714374706.

However, the real random number generator they choice can't generate such large number. I also tested that whether the result is dominated by one of the coefficients (i.e. the secret), and it's not correct.

Also, the order of three x are always same as tho order of y, which means all coefficients are positive.

Based on these result, I guess the coefficients are positive integers. (Another reason is that I have totally no idea how to convert a fraction to a encryption key. LOL)

Underconstrained System of Linear Equations

Now, we have a linear system $Xs = y$ where $X$ is the Vandermonde matrix of those three x. the system is Underconstrained because we have only 3 equations.

Compare to the coefficients, those $y$ are much longer. For such problem, we can solve it with some lattice magic.

However, lattice methods only works with integers. To convert these fractions to integer, I scale up both $X$ and $y$ with $10^{450}$ , and the equations still hold.

Next, I truncate those fractions to integer and concatenate an identity matrix to $X$ . One of the solution becomes $X' [a_0, \cdots, a_4, e_0, e_1, e_2] = y'$ where $e_i$ is the error introduced by truncating. Those error would be smaller than sum of those coefficients because the truncated fractions are smaller than 1.

Finally, I concatenate $y'$ to $X'$ as a column vector, and one of the solution becomes $A [a_0, \cdots, a_4, e_0, e_1, e_2, -1] = 0$

The lattice of solutions is $\{s | As = 0\}$ which can be defined by the right kernel of $A$ .

Alse, the solution we want is quite "short". It's absolute value is about $10^{40}$ compared to others which is about $10^{500}$ .

Finding such vector is hard in general, but we have suboptimal algorithms like LLL. And it guarantees to find the shortest one if it is short enough.

We can solve it with sagemath easily:

A = Matrix([
#  Vandemonde              Identity matrix                    y
    x.list() + [1 if i == j else 0 for j in range(len(y))] + [yi]
    for i, (x, yi) in enumerate(zip(X, y))
    ])
B = A.right_kernel_matrix()
print(-B.LLL()[0])

You can find the full code at here.

The result looks like

a_0: 285450566584795714324161453455178970870,
a_1: 128443615496666315668191505779431802508,
a_2: 120171678482189002974121031567641762737,
a_3: 29169727575576393604385364950262505188,
a_4: 191216618537187805549913252159424580933,
y_s: -1,
e_0: 138021328216454971007230221028671168120,
e_1: 48993614216086579566584094608235291082,
e_2: -85525054552282748747414766196213187078

The last thing is to guess the encryption algorithm, it turns out to be AES CBC with null IV.