I came up with this carbon-neutral cryptosystem and hid my secrets in the forest. Can you help them find their way out?
Time
24 hours
Behavior
In this challenge, we have a encrypted zip and we know the middle of its plaintext.
It use a splay tree based cryptosystem from APPLICATION OF SPLAY TREES TO DATA COMPRESSION.
In short, The state of the cryptosystem is a splay tree with 256 leaves. It encrypts one byte at a time, outputing the path to the leaf of the input byte, and splaying that node.
For example, here's smaller tree:
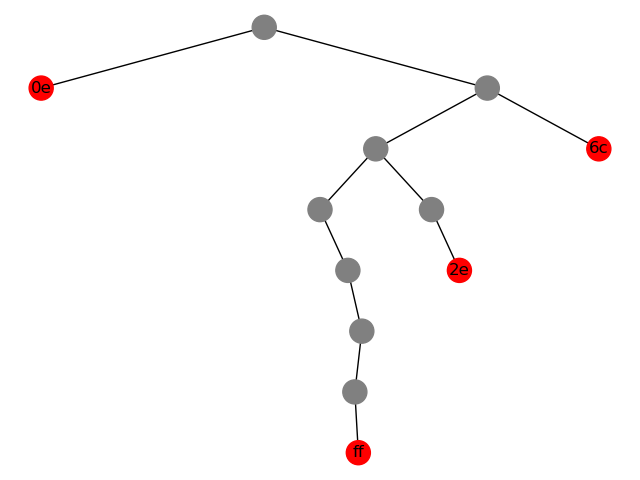
If the input byte is 2e, it outputs 1011. And (the parent of) that leaf is splay to the root.
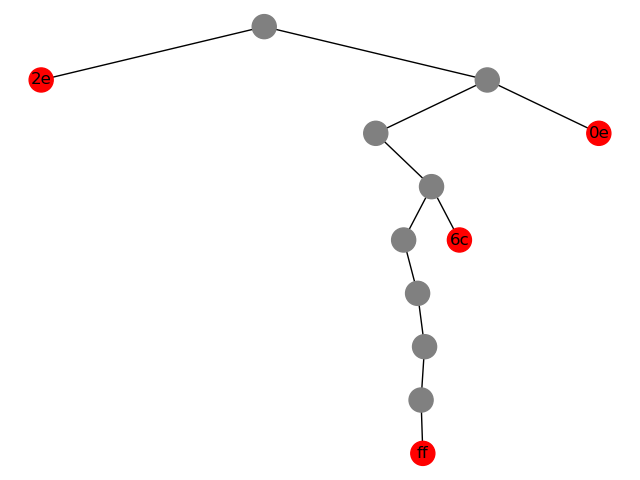
As you can see, the output of each input byte has different length, which is totally a disaster.
Solution
TL;DR
- Find those known plaintext.
- Count the mean and variance of output bit length at each position.
- Reconstruct the splay tree from the end.
- Recover central directory file header.
- Reconstruct local file header based on central directory file header.
- Reconstruct the initial splay tree.
- Decrypt the zip and enjoy the flag.
Known plaintext and statistics
The zip (i.e. plaintext) is generated using:
curl -s -o danny.jpg 'https://www.csd.cs.cmu.edu/sites/.../public/danny-polaroid.jpg'
zip secrets.zip flag-cypress.txt danny.jpg
Here's the diff of two zip files generated from different flag:
1,9c1,9
< 00000000: 2e2e 2e2e 2e2e 2e2e 2e50 4b03 040a 0000 .........PK.....
< 00000010: 0000 0070 bb7f 4e5b 586b 5a33 0000 0033 ...p..N[XkZ3...3
< 00000020: 0000 0010 001c 0066 6c61 672d 6379 7072 .......flag-cypr
< 00000030: 6573 732e 7478 7455 5409 0003 63dc a05c ess.txtUT...c..\
< 00000040: 84dc a05c 7578 0b00 0104 e803 0000 04e8 ...\ux..........
< 00000050: 0300 0050 4354 467b 7765 6c6c 5f69 745f ...PCTF{well_it_
< 00000060: 6973 6e74 5f6d 616e 795f 706f 696e 7473 isnt_many_points
< 00000070: 5f77 6861 745f 6469 645f 796f 755f 6578 _what_did_you_ex
< 00000080: 7065 6374 7d0a 504b 0304 1400 0000 0800 pect}.PK........
---
> 00000000: 504b 0304 0a00 0000 0000 acbb 7f4e 7284 PK...........Nr.
> 00000010: da2e 3c00 0000 3c00 0000 1000 1c00 666c ..<...<.......fl
> 00000020: 6167 2d63 7970 7265 7373 2e74 7874 5554 ag-cypress.txtUT
> 00000030: 0900 03d3 dca0 5cd7 dca0 5c75 780b 0001 ......\...\ux...
> 00000040: 04e8 0300 0004 e803 0000 5043 5446 7b68 ..........PCTF{h
> 00000050: 6d6d 5f73 6f5f 796f 755f 7765 7265 5f41 mm_so_you_were_A
> 00000060: 626c 655f 325f 6730 6c66 5f69 745f 646f ble_2_g0lf_it_do
> 00000070: 776e 3f5f 4865 7265 5f68 6176 655f 615f wn?_Here_have_a_
> 00000080: 666c 6167 7d0a 504b 0304 1400 0000 0800 flag}.PK........
12c12
< 000000b0: 0003 a8dc a05c a8dc a05c 7578 0b00 0104 .....\...\ux....
---
> 000000b0: 0003 a8dc a05c b1dc a05c 7578 0b00 0104 .....\...\ux....
541,542c541,542
< 000021c0: 030a 0000 0000 0070 bb7f 4e5b 586b 5a33 .......p..N[XkZ3
< 000021d0: 0000 0033 0000 0010 0018 0000 0000 0001 ...3............
---
> 000021c0: 030a 0000 0000 00ac bb7f 4e72 84da 2e3c ..........Nr...<
> 000021d0: 0000 003c 0000 0010 0018 0000 0000 0001 ...<............
544c544
< 000021f0: 7072 6573 732e 7478 7455 5405 0003 63dc press.txtUT...c.
---
> 000021f0: 7072 6573 732e 7478 7455 5405 0003 d3dc press.txtUT.....
548c548
< 00002230: 0000 0000 0000 0000 00b4 817d 0000 0064 ...........}...d
---
> 00002230: 0000 0000 0000 0000 00b4 8186 0000 0064 ...............d
552c552
< 00002270: b221 0000 0000 .!....
---
> 00002270: bb21 0000 0000 .!....
The file looks almost the same, which means we could possibly mount known-plaintext attack.
So how about the ciphertext?
11000010011011100111111100011011011010011111100100010111011100100011110001011000
11010010001010100001111111000101011010111001000110001110111100011101010111011000
Some pattern in the string matches, but they aren't aligned well.
If we segment those bits:
P C1 C2 C3 C4
03 1001000 100011010 10010000010 100011
00 1000111 1001011 100011 10100
00 0 0 0 0
04 10011 10011 1010 10010
e8 10011 10011 100 10011
03 10011 10011 1001 10011
00 10011 10011 1010 10011
00 0 0 0 0
50 10010000010 100101100 1010110110000 1001011111000
4b 1000000 10000110 10000000 10000000
05 1001001010 100100101 100100010 1000101111
06 100111010000011 100001111011100 10000010010000101111 10000100000111011
00 100110 1001011 1001111 1001101
00 0 0 0 0
00 0 0 0 0
00 0 0 0 0
02 10011100 10001011000 1000100100 100101111000
00 11 11 11 11
02 11 11 11 11
00 11 11 11 11
a5 100100010011011 100001011100101110 1001100101111100001 1000001101001110101
00 11 11 11 11
00 0 0 0 0
00 0 0 0 0
xx 100000110110110 1000011000101 1001001001100 1000111000010
21 100100110100011000 10001101101 10010001100101 100000110100
00 1011 101 1011 1011
00 0 0 0 0
00 0 0 0 0
00 0 0 0 0
Cool, There is a large bias on the output bit length at each position.
Moreover, those short ones are almost the same. In fact, those 0 and 11 are all the same across all the files we generated.
If we look at the part of compressed image, where the input has larger entropy:
P C1 C2 C3 C4
21 100101010010 10001010 1000110110 10011001111
47 10011001110001101 10010000110010 100010000 1000011010110011
68 1001001111 1001010111100100 100101000111010011100 1000010011
be 1001110000111 10000111101110 100000100111 1001110101110
c2 10000011010010101 100110111100 10001001010010 10001010011110000
21 1001011 101001 10100 1001011
ff 100010101111101110 101010011100010010110 1001111000111111 100101100101010
1f 1000011110101 100010011010 10000011111010 100010101111100
66 10000011111100010 10001111101000001111 100101001101101100 10010010011111
e3 100100101100010010111010 1001100000101 100110101100 1001111000110
b4 1000000101 100100001101 100111000 100001011100001
2f 1001111100110 100110011101111 1001011000 10001011100101100
c0 100000011010 100101111011010 10001011110 100001110
9e 1001100100001110 100001001110001 1000011111110 1001000001000000011011010
93 100000000 1000000010 10000000 10000000000000
ff 100011100 1001100111 1001100001 10001101
37 1000111110001 10010011101 100001100111 10011101111001001
e3 100100100 1001010 1001001 1000101
ee 1001010110111 1001011111001001 100100101000001 100010010010000
d2 100010011111110011 10000001011011 10000100111000101 1000100100111100000111
87 1001010101 1001010000 1000011000 1000010011
a7 1001110010 100101101111010 100110011011100100 1000111010
f6 10000001100 1001011010010 10000011111001 10011110001100100
1b 1000111000010 1000000110101 100010101 1001010000010
05 10010011011100111110 100100111011011 10001111101 1001001110110110111101
91 10000000101000 10010101110010 10010011110011111101011 10011010011
83 10010000111111000100 100011111101000 100001001001110 1000011000
48 100111111010101 10001110111110 10001000011011000 1001100011100011000
23 100010011111101 1001011101101 10000101100111 10000010101
1d 1000101111101 100011010011100000 1001100011101101001 10001110000
The variance become larger, but it seems still has some bias on the output length. Average standard deviation is 2.4 between 400 aligned samples, and 3.6 between shuffled samples.
Another thing we can notice is that those bits has 100 or 101 prefix. Because the splay operation lift the previous byte to the root, it becomes 0, and the second previous bytes becomes 11, Other bytes should starts with 100 or 101. This gives us a great boundary for generating possible segmentations.
Reconstruct the tree
Now, assuming we have the segmentation, how can we reconstruct the splay tree?
If the input is ff and the output is 1001101, which means there's a leaf at 1001101, and all nodes on the path are not leaves. To undo the operation, we build a tree with that path only, connect all other edges to placeholders,
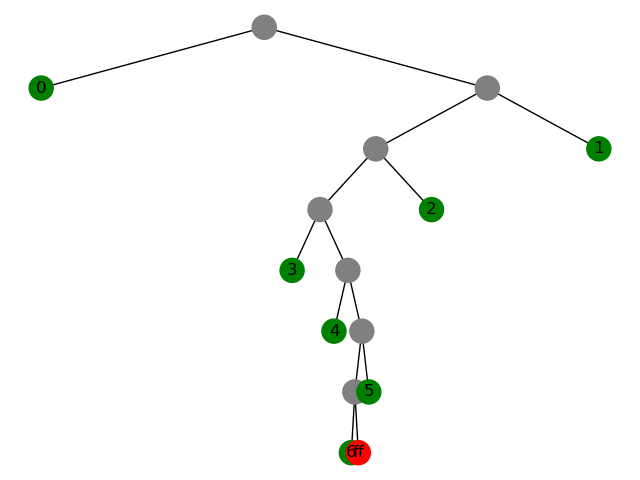
splay the node,
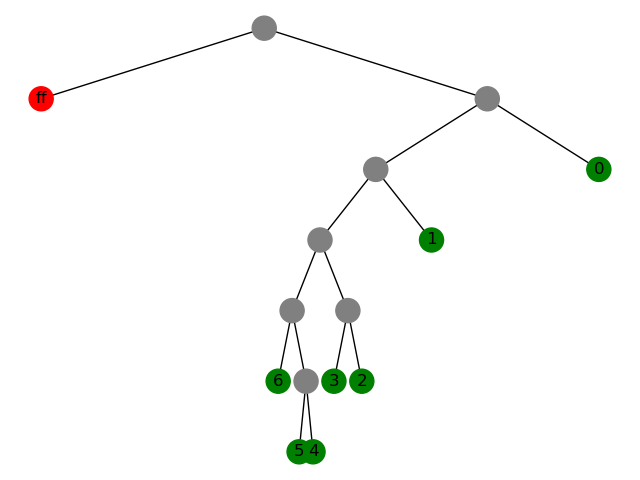
compare to current state,
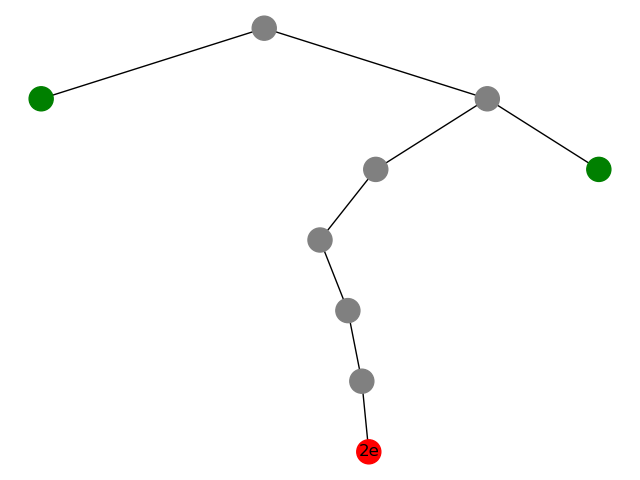
and fill those placeholders before splay.
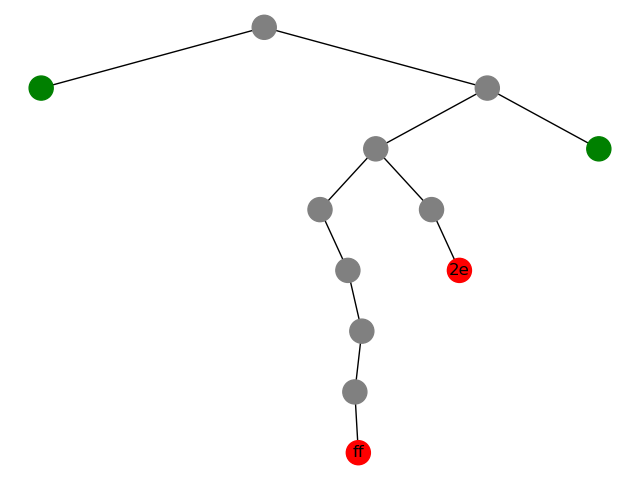
There are some indicator for incorrect segmentation:
- Tree structure does not match
- Type of node does not match (i.e. internal nodes v.s. leaves)
- Tag of leaf does not match
- Duplicated tag of different leaf
- The ciphertext
0and11does not match, which is independent of key.
We can just use dfs to find a valid segmentation.
Speedup the searching progress
When generate the possible segmentation, we only consider segmentation length in range and ordered by the error.
This trick speedup the searching process a lot, from hours to 3 minutes, even with unoptimized python script.
However, not all segmentation length are inside 4 std. We increase the range to 10 std after reconstructing 200 nodes. Since half of the tree is reconstructed, the searching depth of a negative guess is pretty shallow, so the increment doesn't hurt the performance too much.
We also pre-generate a set of ciphertext sequences shorter than 8 with random plaintext, it turns out there are only 50 possible sequences rather than 255.
For longer sequence, we check it has 100 or 101 prefix.
Than's all about the solution's algorithm. Here's the code if you want to take a look.
Now, We are ready to get the flag, really?
Distribution of target plaintext
Using the algorithm described above, we are able to reconstruct the tree of the zip files we generated. However, it failed on the target ciphertext.
The zip files we generated are different from the secret zip. After re-checking the provided script, We found something interesting:
curl -s -o danny.jpg 'https://www.csd.cs.cmu.edu/sites/.../public/danny-polaroid.jpg'
zip secrets.zip flag-cypress.txt danny.jpg
./splaid-cypress -e secrets.zip -o secrets.zip.enc -p "$(cat key-cypress.txt)"
rm -f splaid-cypress.zip
zip splaid-cypress.zip secrets.zip.enc splaid-cypress.sh libsplaid.so.1 splaid-cypress
rm -f secrets.zip secrets.zip.enc danny.jpg
It seems that the task's zip itself is generated from the same environment.
Let's talk about the zip format. Generally, zip file looks like this: (Image from wikipedia) There are Local file header following its data for each file, and a Central directory containing multiple Central directory file header and a End of central directory record (EOCD).
The central directory of task's zip looks like:
Signature: 504b 0102 (Central directory)
Version: 1e03
Min version: 0a00
Flag: 0000
Compression method : 0000
Modification time: f016
Modification date: 4b4e
CRC32: 5a25 57b3
Compressed size: 7c39 0000
Uncompressed size: 7c39 0000
File name length: 0f00
Extra field length: 1800
File comment length: 0000
Disk number where file starts: 0000
Internal file attributes: 0000
External file attributes: 0000 a481
Relative offset of local file header: 0000 0000
File name:
736563726574732e7a69702e656e63
s e c r e t s . z i p . e n c
Extra field:
Signature: 5554 (UT / Extended Timestamp)
Size: 0500
Flags: 03
Modification Time: 24e4 605c
Signature: 7578 (ux / Infozip Unix)
Size: 0b00
Version: 01
Size of UID: 04
UID: 0000 0000
Size of GID: 04
GID: 00 0000 00
File comment:
None
So the version of the zip is 1e03, default file permission is a481, and the uid/gid is 0.
With these information, we generate ciphertext of random time, crc, and size to calculate those statistics info again.
This time, it reconstruct the tree of known plaintext part successfully. However, it still can't reconstruct the flag part.
Leading part of the plaintext
Let's take a look of the best (i.e. longest) plaintext our algorithm recover:
00000000: 3131 310a 310a 3131 310a 0a15 15c9 31c9 111.1.111.....1.
00000010: 0a31 0a0a 3010 3030 3080 8080 3030 3080 .1..0.000...000.
00000020: 8030 1004 c0de 8f58 2de4 e07e 2058 5bf8 .0.....X-..~ X[.
00000030: 024d 4cc0 b888 b920 41fc bb38 ed4c c33c .ML.... A..8.L.<
00000040: 3e62 9082 9dee 262c a9c1 2bd9 fa82 4dd7 >b....&,..+...M.
00000050: f0d7 e22c e1cc 2a84 d243 6857 08b1 0a23 ...,..*..ChW...#
00000060: 8a1c 359b 32b8 5a72 7bbb 0f50 4b03 0414 ..5.2.Zr{..PK...
00000070: 0908 09f0 164b 4ef9 f209 41f2 2009 09b7 .....KN...A. ...
00000080: 2109 0900 1c00 6461 6e6e 792e 6a70 6755 !.....danny.jpgU
00000090: 5409 0003 24e4 605c 24e4 605c 7578 0b00 T...$.`\$.`\ux..
It recover danny.jpg, which is the local file header of danny.
Signature: 504b 0304 (Local file header)
Flag: (Missing)
Min version: 1409
Compression method: 0809
Modification time: f016
Modification date: 4b4e
CRC32: f9f2 0941
Compressed size: f220 0909
Uncompressed size: b721 0909
File name length: 001c
Extra field length: 0064
File name:
64616e6e792e6a7067
d a n n y . j p g
Extra field:
Signature: 5554 (UT / Extended Timestamp)
Size: 0900
Flags: 03
Modification Time: 24e4 605c
Access Time: 24e4 605c
Signature: 7578 (ux / Infozip Unix)
Size: 0b00
Version: 01
Size of UID: 04
UID: 0000 0000
Size of GID: 04
GID: 0000 0000
Some 00 decoded as 09 incorrectly, and the flag field disappeared.
In fact, we know what those information should be. Most of them are in the central directory, and we have already recovered them. The compressed size of the flag is also in central directory, and it's 79 bytes. Again, we regenerate the known plaintext, the statistics info, and run again.
There are some bugs in our code on the boundary condition, it does not terminate correctly.
But when we take the longest plaintext, remove the leading junk, it decompressed successfully. Great, 600 points after 24 hours with hundreds lines of code.
It was my first time breaking a cryptosystem without any help from existing paper, Thanks PPP for such a nice and interesting challenge :)


