Reverse a cellular automata

Attachmentscrypto - 80148 solves

It's hard to reverse a step in a cellular automata, but solvable if done right.

Time

15 minutes

Behavior

We have built a cellular automata with 64 bit steps and obeys Wolfram rule 126, it's boundary condition wraps around so that the last bit is a neighbor of the first bit. Below you can find a special step we chose from the automata.
The flag is encrypted with AES256-CBC, the encryption key is the previous step that generates the given step. Your task is to reverse the given step and find the encryption key.
Obtained step (in hex)
66de3c1bf87fdfcf

We got a state of cellular automata, and we have to find its previous state.

Solution

TL;DR

  1. Use DFS to find the key
  2. Decrypt the flag with all those key
  3. Find the flag which contains CTF.

The rule 126 is:

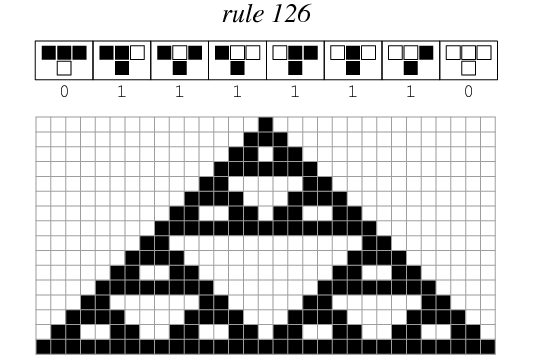
Rule 126

For example, if the neighbors (include itself) of a bit is 000, it becomes 1 in the next step.

To search for a solution, we iterate throught possible -1, 0, 1 bits based on the first bit. And then we use DFS to set all those middle bits. Finally, we check that the head is consistant with the tail, and try to decrypt the flag with it.

You can find the code in here.